Introducing the Kasparian Solids

By Raffi J. Kasparian, Annandale, Virginia USA

This paper serves as an introduction to a newly discovered type of polyhedron. It will briefly discuss the history of polyhedra discoveries and culminate with a discussion of the Kasparian solids which are members of a new class of solid dubbed by their discoverer, the "Rational" solids.

Definitions

Polyhedron

A polyhedron is a three dimensional convex shape or surface formed of polygons joined together at an edge. Cubes and pyramids are simple and common examples of polyhedra.

Cube Four-sided Pyramid

Regular Polyhedron

A regular polyhedron is a polyhedron whose surface is made up entirely of regular polygons. Additionally, each vertex of a regular polyhedron is formed of the same combination of regular polygons. A cube is the most well known example of a regular polyhedron made up of only one polygon type. Each vertex of a cube is formed by three squares. Perhaps the most well known example of a regular polyhedron made from more than one type of polygon is the Truncated Icosohedron of which the common soccer ball is an example. Each vertex of the truncated icosohedron is formed by two hexagons and one pentagon.

Cube Truncated Icosohedron

A Brief History of Polyhedron Discoveries

This discussion will approach the discovery of new polyhedra as definitions were gradually expanded and assumptions cast off, starting with the first discovered solids.

Platonic Solids

Credit for the discovery of all possible regular polyhedra that use only one polygon type is given to Plato. They were certainly all discovered by the 5th century BC. Known as the Platonic solids, there are only five. They are the Tetrahedron made of three triangles at each vertex, the Cube made of three squares at each vertex, the Octahedron made of four triangles at each vertex, the Dodecahedron made of three pentagons at each vertex and the Icosahedron made of five triangles at each vertex.

We will use a simple notation for the regular polyhedra that lists the types of polygons at a vertex, separated by a comma and surrounded by curly brackets. We'll call this the "signature" of a regular polyhedron.

Solid Name Signature Click Image to View in Archimedean
Tetrahedron {3,3,3}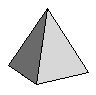
Cube {4,4,4}
Octahedron {3,3,3,3}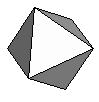
Dodecahedron {5,5,5}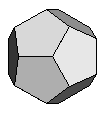
Icosahedron {3,3,3,3,3}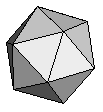

Platonic Requirements

Archimedean Solids

Archimedes, in the 3rd century BC, discovered 13 regular polyhedra made of different polygon types in which the requirement that only one polygon type be used is relaxed.

Solid Name Signature Click Image to View in Archimedean
Truncated Tetrahedron {3,6,6}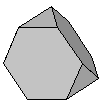
Truncated Cube {3,8,8}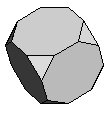
Truncated Octahedron {4,6,6}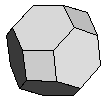
Cuboctahedron {3,4,3,4}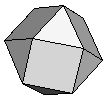
Small Rhombicuboctahedron {3,4,4,4}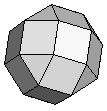
Truncated Cuboctahedron {4,6,8}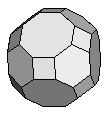
Snub Cube {3,3,3,3,4}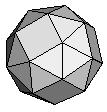
Truncated Dodecahedron {3,10,10}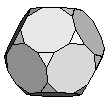
Truncated Icosahedron {5,6,6}
Icosidodecahedron {3,5,3,5}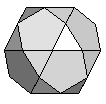
Small Rhombicosidodecahedron {3,4,5,4}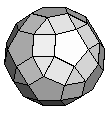
Truncated Rhombicosidodecahedron {4,6,10}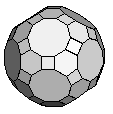
Snub Dodecahedron {3,3,3,3,5}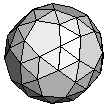

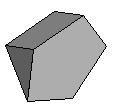
There is also a class of polyhedra known as the prisms and antiprisms of which there is an infinite variety. Technically, they conform to the definition of an Archimedean solid but they are not generally included with them. Prisms are formed of two squares and any other single polygon. Antiprisms are formed of three triangles and any other single polygon.

Solid Name Signature Click Images to View in Archimedean
Prism {4,4,*} etc.
Antiprism {3,3,3,*} etc.

Archimedean Requirements

Kepler Solids

In 1619 AD, Johannes Kepler discovered two more solids by casting off the assumption that a regular polygon must be convex and also relaxing the requirement that sides shouldn't intersect. By joining pentagrams (the five pointed star known alternately as a star pentagon) three at a vertex, he discovered the Great Stellated Dodecahedron and by joining them five to a vertex, the Small Stellated Dodecahedron. These are known as the Kepler solids.

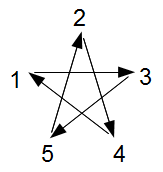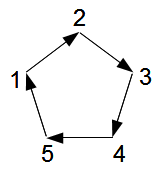
A pentagram is an example of what is known as a star polygon. Star polygons are notated as a fraction with the numerator representing the number of points and the denominator representing how to connect the points. A standard pentagram is represented as 5/2, meaning that there are five vertices, each vertex connected by a line to the second vertex away (counting clockwise). A regular pentagon could be represented as 5/1, but this just reduces to 5.

Regular Pentagon (5/1)
Five vertices, five edges 		Star Pentagon (5/2)
Five vertices, five edges

Solid Name Signature Click Image to View in Archimedean Building one Vertex
Great Stellated Dodecahedron {5/2,5/2,5/2}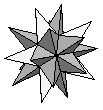
One Pentagram Two Pentagrams Three Pentagrams
Small Stellated Dodecahedron {5/2,5/2,5/2,5/2,5/2}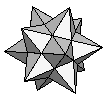
One Pentagram Two Pentagrams Three Pentagrams Four Pentagrams Five Pentagrams

Kepler Requirements

Poinsot Solids

In 1809, by allowing regular polygons to intersect each other, Louis Poinsot discovered the Great Dodecahedron which is made of 5 pentagons at each vertex, circumnavigating the vertex twice before joining up, and the Great Icosahedron which is made of 5 triangles at each vertex also circumnavigating the vertex twice before joining up. These are known as the Poinsot solids. The Poinsot solids are very closely related to the Kepler solids and they are often referred to collectively as the Kepler-Poinsot solids.

We extend the syntax of a signature to represent how many times a corner is circumnavigated before its sides join. Similar to the notation for star polygons, the entire signature is treated like a fraction with the numerator representing the polygons at a corner and the denominator representing the circumlocutions.

Solid Name Signature Click Image to View in Archimedean Building one Vertex
Great Dodecahedron {5,5,5,5,5}/2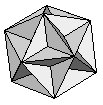
One Pentagon Two Pentagons Three Pentagons Four Pentagons Five Pentagons
Great Icosahedron {3,3,3,3,3}/2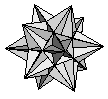
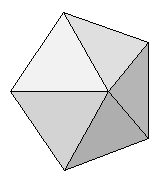
One Triangle Two Triangles Three Triangles Four Triangles Five Triangles

Poinsot Requirements

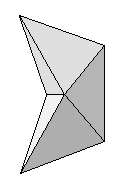It should be noted that the rule of convex corners has been somewhat compromised with the Poinsot solids. Looked at as a whole, these corners are not completely convex, due to the fact that sides intersect each other as they circumnavigate each vertex a second time. However, it is still the case that wherever sides are joined, they are joined to each other in a convex manner, meaning that each joined side angles closer towards the center of the polyhedron.

5 convex joins 4 convex joins
1 concave join

Nonregular Star Polyhedra

From the year 1878 - 1947, by relaxing every requirement except that all corners be the same, 53 more solids were discovered (and rediscovered) by various mathematicians including Edmund Hess (1878), Albert Badoureau (1881), Pitsch (1881), H.S.M. Coxeter and J. C. P. Miller (1930–1932), M.S. Longuet-Higgins and H.C. Longuet-Higgins. These are collectively known as the nonregular star polyhedra.

Solid Name Signature Click Image to View in Archimedean
Great Cubicuboctahedron {8/3,3,8/3,4}
Cubitruncated Cuboctahedron {8/3,6,8}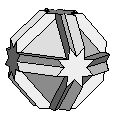
Stellated Truncated Hexahedron {8/3,8/3,3}
Great Truncated Cuboctahedron {8/3,4,6}
Small Ditrigonal Icosidodecahedron {5/2,3,5/2,3,5/2,3}
Small Icosicosidodecahedron {6,5/2,6,3}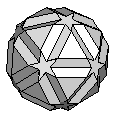
Small Snub Icosicosidodecahedron {3,5/2,3,3,3,3}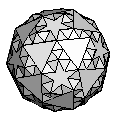
Dodecadodecahedron {5/2,5,5/2,5}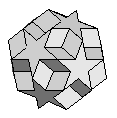
Truncated Great Dodecahedron {10,10,5/2}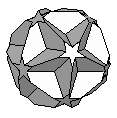
Rhombidodecadodecahedron {4,5/2,4,5}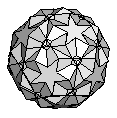
Snub Dodecadodecahedron {3,3,5/2,3,5}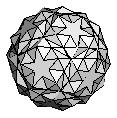
Great Ditrigonal Dodecicosidodecahedron {10/3,3,10/3,5}
Icositruncated Dodecadodecahedron {10/3,6,10}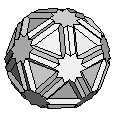
Great Icosidodecahedron {5/2,3,5/2,3}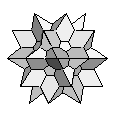
Great Truncated Icosahedron {6,6,5/2}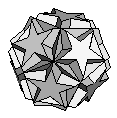
Great Snub Icosidodecahedron {3,3,5/2,3,3}
Small Stellated Truncated Dodecahedron {10/3,10/3,5}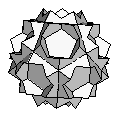
Truncated Dodecadodecahedron {10/3,4,10}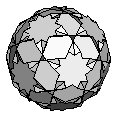
Great Dodecicosidodecahedron {10/3,5/2,10/3,3}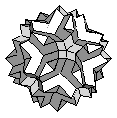
Great Stellated Truncated Dodecahedron {10/3,10/3,3}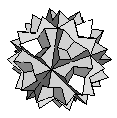
Great Truncated Icosidodecahedron {10/3,4,6}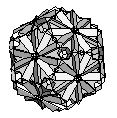
Great Retrosnub Icosidodecahedron {3,3,3,3,5/2}/2
Great Ditrigonal Icosidodecahedron {3,5,3,5,3,5}/2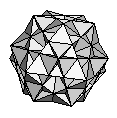
Octahemioctahedron {6,3/2,6,3}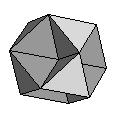
Tetrahemihexahedron {4,3/2,4,3}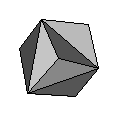
Small Cubicuboctahedron {8,3/2,8,4}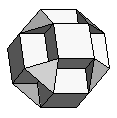
Cubohemioctahedron {6,4/3,6,4}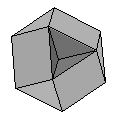
Great Rhombicuboctahedron {4,3/2,4,4}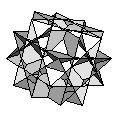
Small Rhombihexahedron {8,4,8/7,4/3}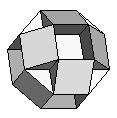
Small Dodecicosidodecahedron {10,3/2,10,5}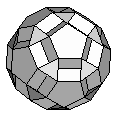
Small Rhombidodecahedron {10,4,10/9,4/3}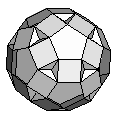
Great Icosicosidodecahedron {6,3/2,6,5}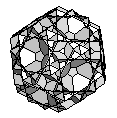
Small Icosihemidodecahedron {10,3/2,10,3}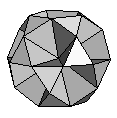
Small Dodecicosahedron {10,6,10/9,6/5}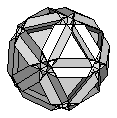
Small Dodecahemidodecahedron {10,5/4,10,5}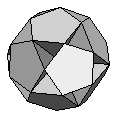
Rhombicosahedron {6,4,6/5,4/3}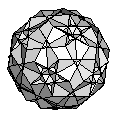
Great Dodecahemicosahedron {6,5/4,6,5}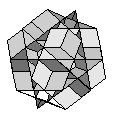
Great Rhombihexahedron {4,8/3,4/3,8/5}
Ditrigonal Dodecadodecahedron {5/3,5,5/3,5,5/3,5}
Small Ditrigonal Dodecicosidodecahedron {10,5/3,10,3}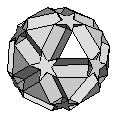
Icosidodecadodecahedron {6,5/3,6,5}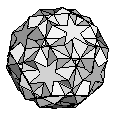
Snub Icosidodecadodecahedron {3,5/3,3,3,3,5}
Inverted Snub Dodecadodecahedron {3,5/3,3,3,5}
Small Dodecahemicosahedron {6,5/3,6,5/2}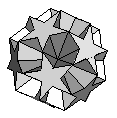
Great Dodecicosahedron {6,10/3,6/5,10/7}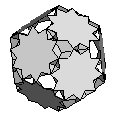
Great Snub Dodecicosidodecahedron {3,5/3,3,5/2,3,3}
Great Rhombicosidodecahedron {4,5/3,4,3}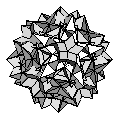
Great Inverted Snub Icosidodecahedron {3,5/3,3,3,3}
Great Dodecahemidodecahedron {10/3,5/3,10/3,5/2}
Great Icosihemidodecahedron {10/3,3/2,10/3,3}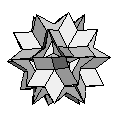
Small Retrosnub Icosicosidodecahedron {3,3,3,3,3,5/3}/2
Great Rhombidodecahedron {4,10/3,4/3,10/7}
Great Dirhombicosidodecahedron {4,5/3,4,3,4,5/2,4,3/2}/2

Nonregular Star Polyhedra Requirements

In 1970, Ukrainskiui Geometricheskiui Sbornik proved that all possible nonregular star polyhedra built according to these requirements had been discovered.

Johnson Solids

In 1966, Norman Johnson discovered 92 more polyhedra by relaxing the requirement that the vertices be the same. Here is a sampling of the many Johnson solids.

Solid Name Johnson Code  
Elongated Square Cupola J19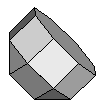
Metabidiminished Icosahedron J62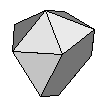
Tridiminished Rhombicosidodecahedron J83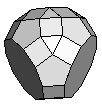

Johnson Requirements

Later explorations into polyhedra took more abstract routes including polyhedra in multiple dimensions, and polygons formed of curves rather than straight lines.

Kasparian Solids

Kasparian Solids were discovered by Raffi Jacques Kasparian in 1998 while writing a virtual polyhedra construction tool, named "Archimedean", designed to build polyhedra where all corners match an arbitrary given definition. Its method was to build one corner according to the given definition and then to continue to propogate corners until all unconnected edges joined with preexisting edges. As more and more corners were built in this manner, the prospective solid would gradually become a quasi-spherical shell. If there was no way to complete the solid before sides began to intersect each other, construction would be abandoned. On the other hand, if all edges eventually joined before any sides intersected, then the solid would be complete and would have been empirically proven to exist. During the process of development of Archimedean, it was discovered that some unrecognized solids could be constructed if sides were allowed to traverse the quasi-spherical shell more than once in their attempt to complete the solid. Kasparian solids are the result of relaxing the tacit assumption that the sides of a polyhedron may traverse the quasi-spherical shell only once in an attempt to join all edges.

Sides intersect in the Kasparian solids as they do in other solids but they differ in the manner in which they intersect. In Poinsot solids and some of the star polyhedra, sides intersect as they form a corner by circumnavigating the vertex twice before joining each other. In many of the star polyhedra, sides intersect because the sides themselves are made from polygons with intersecting line segments. In Kasparian solids, sides intersect each other because they circumnavigate the surface of the solid more than once before finally joining each other. While it is easy to quantify the number of times sides circumnavigate a vertex, it is less obvious how to quantify the number of times the sides circumnavigate a surface. This new class of solid is dubbed "Rational" because it seems self-evident that whatever the eventual method for counting circumnavigations, the sides certainly circumnavigate the surface a rational number of times.

Once again we extend the syntax of a signature. Appending a plus sign signifies that sides circumnavigate the surface more than once.

Kasparian Code Signature Click Image to View in Archimedean One Corner
Click to Play Construction Animation 		Edges
K1 {3,3,4}+ 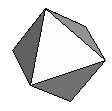12:(3, 3, 4)
K2 {3,4,5}+ 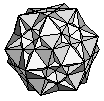60:(3, 4, 5)
K3 {3,4,6}+ 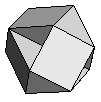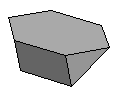24:(3, 4, 6)
K4 {3,5,5}+ 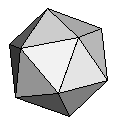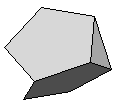30:(3, 3, 5, 5)
K5 {3,5,10}+ 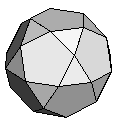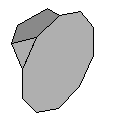60:(3, 5, 10)
K6 {3,6,10}+ 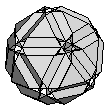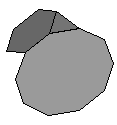60:(3, 6, 10)
60:(6, 10)
K7 {4,5,6}+ 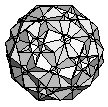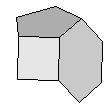60:(4, 5, 6)
60:(4, 6)
K8 {4,5,10}+ 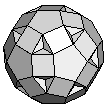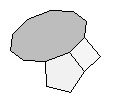60:(4, 5, 10)
60:(4, 10)
K9 {3,4,8}+ 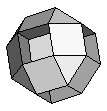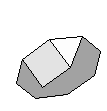24:(3, 4, 8)
24:(4, 8)
K10 {3,4,10}+ 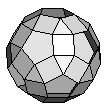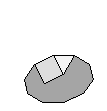60:(3, 4, 10)
60:(4, 10)

Kasparian Requirements

Unlike the previously discussed solids, edges are often shared by more than 2 sides in the Kasparian solids.

K1 Every edge is shared by two triangles and one square. (3, 3, 4)
K2 Every edge is shared by one triangle, one square and one pentagon. (3, 4, 5)
K3 Every edge is shared by one triangle, one square and one hexagon. (3, 4, 6)
K4 Every edge is shared by two triangles and two pentagons. (3, 3, 5, 5)
K5 Every edge is shared by one triangle, one pentagon and one decagon. (3, 5, 10)
K6 Some edges are shared by one triangle, one hexagon and one decagon. (3, 6, 10)
Other edges are shared by only one hexagon and one decagon. (6, 10)
K7 Some edges are shared by one square, one pentagon and one hexagon. (4, 5, 6)
Other edges are shared by only one square and one hexagon. (4, 6)
K8 Some edges are shared by one square, one pentagon and one decagon. (4, 5, 10)
Other edges are shared by only one square and one decagon. (4, 10)
K9 Some edges are shared by one triangle, one square and one octagon. (3, 4, 8)
Other edges are shared by only one square and one octagon. (4, 8)
K10 Some edges are shared by one triangle, one square and one decagon. (3, 4, 10)
Other edges are shared by only one square and one decagon. (4, 10)

A Bit of Analysis


K1 is much like the Octahedron with 3 additional squares spanning the square spaces that naturally occur inside an Octahedron,
= +
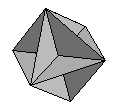K1 Octahedron 3 squares

and K5 is much like the Icosidodecahedron with the addition of 6 decagons spanning the decagonal spaces that naturally occur inside an Icosidodecahedron.
= +
K5 Icosidodecahedron 6 decagons

K4 can be decomposed into two known solids, the Icosahedron and the Great Dodecahedron.
= +
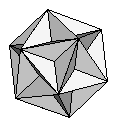K4   Icosahedron   Great Dodecahedron

K3 shares the same vertices as the Cuboctahedron but connects them differently,
≈
K3   Cuboctahedron

and K8 shares the same vertices as the Small Rhombicosidodecahedron but connects them differently.
≈
K8   Small Rhombicosidodecahedron

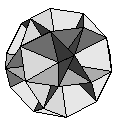
K2 contains within it 5 cubes plus an inner framework of pentagons and a shell with pentagonal holes that is made of intesecting triangles,
= + +
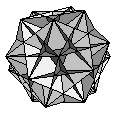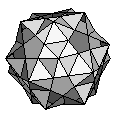K2   5 cubes   12 pentagons   30 intesecting triangles

and it shares the same vertices as the Great Ditrigonal Icosidodecahedron but connects them differently.
≈
K2   Great Ditrigonal Icosidodecahedron

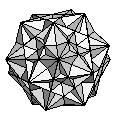
As far as my analysis has taken me, K6, K7, K9 and K10 do not contain within themselves any convex polyhedra. They do share the same vertices as some of the non-Rational polyhedra.
≈ , ,
K6   Small Icosicosidodecahedron Small Dodecicosahedron Small Ditrigonal Dodecicosidodecahedron

≈ , , ,
K7   Small Snub Icosicosidodecahedron Rhombidodecadodecahedron Rhombicosahedron Icosidodecadodecahedron

≈
K9   Small Rhombicuboctahedron

≈
K10   Small Rhombicosidodecahedron

Further Exploration

Recently, I have written code so that Archidean can systematically explore other possible Rational solid signatures. So far, the results have yielded the following polyhedra. It is interesting that no Rational solid discovery has yet produced a solid whose vertex coordinates are not the same as at least one non-Rational solid.

Signature Click Image to View in Archimedean Analysis Edges
{3,3,5}+ 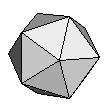= Great Dodecahedron + Icosahedron
≈ K4 		30:(3, 3, 5, 5)
{3,4,10/3}+ 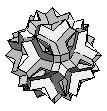≈ Great Rhombidodecahedron 60:(3, 4, 10/3)
60:(4, 10/3)
{5/2,10/3,4}+ ≈ Great Rhombidodecahedron 120:(4, 5/2, 10/3)
{3,5/2,10/3}+ 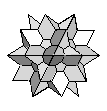≈ Great Icosihemidodecahedron 60:(3, 5/2, 10/3)
{3,8/3,4}+ ≈ Great Cubicuboctahedron 24:(3, 4, 8/3)
24:(4, 8/3)
{3,10/3,6}+ 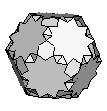≈ Great Ditrigonal Dodecicosidodecahedron 60:(3, 6, 10/3)
60:(6, 10/3)
{5,6,10/3}+ 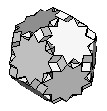≈ Great Ditrigonal Dodecicosidodecahedron 60:(5, 6, 10/3)
60:(6, 10/3)
{4,5/2,6}+ ≈ Rhombidodecadodecahedron 60:(4, 6, 5/2)
60:(4, 6)
{5,6,5/2}+ 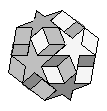= Dodecadodecahedron + 10 hexagons 60:(5, 6, 5/2)
{6,5/2,10}+ 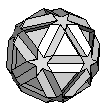≈ Small Icosicosidodecahedron, Small Dodecicosahedron, Small Ditrigonal Dodecicosidodecahedron, K6 60:(6, 10, 5/2)
60:(6, 10)
{4,5/2,5}+ ≈ Ditrigonal Dodecadodecahedron
contains 5 cubes 		60:(4, 4, 5, 5/2)

The following solids are grouped into families of identical polyhedra. They illustrate that multiple signatures can sometimes arrive at the same end result.

Family Signature Click Image to View in Archimedean Analysis Edges
A {3,3,5/2}+ = Small Stellated Dodecahedron + Great Icosahedron 30:(3, 3, 5, 5)
{5/2,5/2,3}+ = Small Stellated Dodecahedron + Great Icosahedron 30:(3, 3, 5, 5)
{3,5/2,5/2,5/2}+ = Small Stellated Dodecahedron + Great Icosahedron
Irregularities in building point
to a possible bug in Archimedean. 		(3, 3, 5, 5)
(3, 5, 5)
B {3,5,3,5/2}+ ≈ Ditrigonal Dodecadodecahedron 60:(3, 5, 5/2)
{5/2,3,5/2,5}+ ≈ Ditrigonal Dodecadodecahedron 60:(3, 5, 5/2)
C {3,4,4,5/2}+ ≈ Ditrigonal Dodecadodecahedron
contains 5 cubes 		60:(3, 4, 4, 5/2)
{3,4,5/2,4}+ ≈ Ditrigonal Dodecadodecahedron
contains 5 cubes 		60:(3, 4, 4, 5/2)
{3,5/2,4}+ ≈ Ditrigonal Dodecadodecahedron
contains 5 cubes 		60:(3, 4, 4, 5/2)
{3,4,5/2,3,5/2}+ ≈ Ditrigonal Dodecadodecahedron
contains 5 partial cubes
Irregularities in building point
to a possible bug in Archimedean. 		(3, 4, 4, 5/2)
(3, 4, 5/2)

Extended Kasparian Requirements