Figure 1. Side View of Window and 3D Object
| Raffi Kasparian <quantime2007@cox.net> has been programming on the Macintosh as a hobby since 1990 when he bought his first Mac (an SE). Languages include Pascal, C, C++ and Java. He won the Mactech Programmers' Challenge in July 1993 and again in May 1995. He holds his degrees in music (piano performance) and earns his living as a classical pianist. |
Figure 1. Side View of Window and 3D Object
This situation is analogous to a computer drawing 3D images onto a 2D video screen. Before we proceed, please take a moment to familiarize yourself with the orientation of the 3D axes with respect to a computer screen (Figure 2) . When looking straight at the screen, the x-axis is horizontal and increases to the right, the y-axis is the depth axis and increases as it moves away from the viewer, and the z-axis is vertical and increases as it moves up. Be sure to contrast this with the standard computer screen 2D axes (Figure 3) where the x-axis is horizontal and increases to the right, the y-axis is vertical and increases downwards and the origin (0, 0) is the top left corner of the screen.
Figure 2. 3D Axes When Looking Straight at the Screen
Figure 3. Local 2D Axes When Looking Straight at the Screen
Figure 4 below is a slight modification of Figure 1. In it, the window has been replaced by a video screen and the house is now a virtual 3D object. We are looking at the screen from its side which puts the real world to its left and the virtual world to its right. The horizontal line is our depth or y-axis and the vertical line is our height or z-axis. We ignore the width axis (x) for the moment which would be the distance away from this very page you are reading. For convenience, we place our screen on the y = 0 plane and our viewer on the y-axis. Point v represents the viewer's eye, p is a point on the 3D image and p' is the point on the screen where the computer will draw p. Points behind the screen have positive y-coordinates while points in front of the screen have negative y-coordinates. So, for example, vy is negative, py is positive and p'y = 0. Figure 5 is a view of the same situation from above allowing us to see the x-axis.
Figure 4. Side View of Video Screen and Virtual 3D Object
Figure 5. Aerial View of Video Screen and Virtual 3D Object
To map a 3D point p on the house to a 2D point p' on the screen, we imagine a straight line from point p to the user's eye. Point p' is located on the screen at the intersection of this virtual sight line and the screen. As a matter of fact, all 3D points located on this sight line are mapped to the one 2D point where this sight line intersects the screen. Some computer programs incorrectly assume that sight lines are parallel to the depth axis resulting in an incorrect mapping of 3D points to screen points.
p'x/px = vy/(vy - py) From the law of similar triangles. (Refer to Figure 5.)We have now computed the 3D coordinates of p' (p' x, p' y, p' z), but further transformation is required to put our point p' into local screen coordinates. Since the computer's 2D origin is the top left corner of the screen and since its vertical axis increases downwards,
p'x = pxvy/(vy - py) Solving for p'x.
p'y = 0 By definition.
p'z/pz = vy/(vy - py) From the law of similar triangles. (Refer to Figure 4.)
p'z = pzvy/(vy - py) Solving for p'z.
p'screenx = p'x + originx and p'screeny = -p'z + originy.The conversion from 3D coordinates to 2D screen coordinates is implemented by SpacePoint.toScreenCoord() which is called for each point of the object whenever the object has been rotated and needs to be redrawn.
| SpacePoint.toScreenCoord
class OrderedTriple{
//a class to represent a 3D coordinate
static OrderedTriple origin = new OrderedTriple(0,
0, 0);
public OrderedTriple(double x, double y, double z){
//3D coordinate with the ability to map to the 2D screen
//the 2D screen coordinates of the 3D origin which happens to
be located on the screen
//the 3D coordinates of the person viewing the screen
//Convert a 3D coordinate to its 2D screen coordinates |
Figure 6. A 3D Virtual Clock Before and After Rotation
To answer this question let's consider the 3D image of a clock (Figure 6). In Frame 1, the clock's back is facing the user and the user's goal is to rotate the clock to its normal position. First, he drags in a straight line from a to b as depicted in frame 1. As expected, the clock turns over to face the user (Frame 2). He then notices that the clock is upside down. If he drags in a straight line from b back to a exactly reversing his path, we would expect the clock to return to its original position. If however, he drags in a semi-circle from b to a as depicted in Frame 2 we would expect the clock to rotate counter-clockwise to the position in Frame 3. Some computer programs would bring the clock back to its original orientation in both cases reasoning that the cursor returned to its starting position and it doesn't matter where it went in between. In a 2D world this logic would be correct but it is obviously undesirable in the 3D world. We therefore conclude that an object's position after rotation depends on the final position of the cursor as well as the path it took to get there.
Figure 7. How the Mouse's Path is Approximated
| DrawingCanvas.mouseDown
//A drawing surface that knows how to draw 3D objects
//A DrawingCanvas class member that remembers the last 3D
coordinates of the
//When a mousedown occurs, find out and remember what point
on the object's
//A DrawingCanvas class member whose implementation is left
up to the individual
//Calculate what 3D point on the object's surface corresponds
to the screen coordinates
//We will return surfacePoint
//Set cursorPoint to the 3D coordinates of the cursor
for every face f of theSolid{
//We'll talk about this later OrderedTriple.sectPlaneLine
//Find the 3D coordinates of the intersection of the plane
containing points P1, P2, P3
//Two distinct points on the line class SmartPolygon{
//Determine whether or not a point is inside the polygon
based on the reasoning that
int prevdir = 0, postdir = 0, crossings = 0;
start++;
//for every edge (p1x, p1y) -> (p2x, p2y)
if(p1x == p2x && p1y == p2y)
continue;
//that is real
//and x is between the endpoints
//and continues in the same direction as the
edge ending on y and crosses y to |
| DrawingCanvas.mouseDrag
//A DrawingCanvas class member that remembers the distance of
lastCoord from the
//When the cursor has been dragged, calculate where the selected
point on the object's
//map the new cursor location to a 3D point on the "sphere
of influence"
rotateTheSolid(lastCoord, newCoord);
//We'll talk about this later DrawingCanvas.toSphericalCoord
//A DrawingCanvas class member. True if the cursor is
mapped to a point on the back
//Calculate the 3D point on the surface of a sphere with
radius R and center at the
//3D coordinates of the cursor
//intersect the line from the viewer to the cursor with the
sphere
//If the line doesn't intersect the sphere then return the
point on the largest visible
}else{
//Find the intersection(s) of the sphere with radius length r
and center at point c and
OrderedTriple v = b.minus(a);
try{
OrderedTriple.solveQuadratic
//For the quadratic equation ax2 + bx + c = 0 return (-b
± *(b2 - 4ac)) / 2a
double roots[];
double d = Math.sqrt(d2);
double r1 = (-b + d)/(2*a);
|
Premise 1. The location and orientation of an object are completely determined from the location of any three distinct non-collinear points on it or in its space.Premise 2. If an object has been rotated, the pre-rotation and post-rotation coordinates of any three distinct non-collinear points p1, p2 and p3 on the object or in its space are sufficient to determine the precise rotation of the object.
pre-rotation --> post-rotationLet p1 be the point on the surface of the object that the user manipulates with the mouse. Its pre- and post-rotation coordinates a and d were determined in the previous section.
p1: (ax, ay, az) --> (dx, dy, dz)
p2: (bx, by, bz) --> (ex, ey, ez)
p3: (cx, cy, cz) --> (fx, fy, fz)
Figure 8. Graphic View of the Parameters of Rotation
Premise 3. For any desired rotation of an object about the origin, there is a unique 3X3 matrix that can multiply the pre-rotation coordinates of every point to yield its post-rotation coordinates.Matrix multiplication is a common way for a computer program to rotate a 3D object. One simply multiplies the pre-rotation coordinates of every one of the object's vertices by a matrix to yield its post-rotation coordinates. From Premises 1, 2 and 3, it follows that if we can find one 3X3 matrix M that transforms the pre-rotation coordinates of p1, p2 and p3 to their respective post-rotation coordinates, then M will be the desired unique rotation matrix. Here is the logic that will enable us to find M from the pre- and post-rotation coordinates of p1, p2 and p3:
M's desired properties:Unfortunately, not all matrices have unique inverses so we must be careful in choosing p1, p2 and p3 to guarantee the existence of a unique inverse of P. Since the existence of M is predicated on the rotation being around the origin, we can't consider the origin in our computations. Nor can we consider any pair of points that is collinear with the origin. So, p1 and p2 are useful but we must choose a p3 other than the origin. Since any point that is in a definable position with respect to p1 and p2's pre-rotation coordinates will, after rotation, be in that same definable position with respect to their post-rotation coordinates, we'll set p3 to p1 X p2. This sets p3's pre-rotation coordinates c to a X b and its post-rotation coordinates f to d X e. Now that we have calculated a, b, c, d, e, and f, we can solve for M.
M(a x , a y , a z ) = (d x , d y , d z )
M(b x , b y , b z ) = (e x , e y , e z )
M(c x , c y , c z ) = (f x , f y , f z )
All variables except M are known, so we simply solve for M:
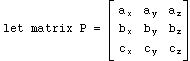
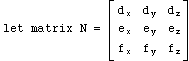
MP = N by substitution into M's desired properties
MPP-1 = NP-1 multiplying both sides of the equation by the inverse of P
MI = NP-1 since any matrix times its inverse equals the identity matrix
M = NP-1 since any matrix times the identity matrix equals itself
|
Quick3X3Matrix.findRotationMatrix
//A streamlined matrix specializing in rotating 3D coordinates
about the origin
//find a matrix M that will rotate the coordinate space
around the origin to bring p1 to
//Find the pre- and post-rotation coordinates of a second
point. We will choose a
//Find the pre- and post-rotation coordinates of a third
point.
//Use Matrix algebra to determine the rotation
matrix
|
Having determined the correct rotation matrix, we may now rotate the
solid.
|
DrawingCanvas.rotateTheSolid
//Rotate the solid from lastCoord to newCoord according to
the user's expectations.
Quick3X3Matrix M =
Quick3X3Matrix.findRotationMatrix(
//rotate theSolid Quick3X3Matrix.times
//A streamlined method that treats an OrderedTriple like a
matrix to multiply it. |
Figure 9. Correcting an Out-Of-Bounds Mouse Path
Figure 10. The Largest Visible Cross Section
If we consider Figure 11, we can calculate the radius length r and the center point d of the largest visible cross section. The sphere has radius length R and center at the origin. Point v is the viewer. R and v are known.
Figure 11. Determining the Largest Visible Cross Section
dy/R = R/vy law of similar trianglesThe largest visible cross section of the sphere is a circle on the plane y = dy with center at (0, dy, 0) and radius of r.
dy = R2/vy solving for d
dy2 + r2 = R2 Pythagorean theorem
r = *(R2 - dy2) solving for r
| DrawingCanvas.outOfBoundsMouseDrag
//A DrawingCanvas class member. True if the cursor
directly maps to a point on the
//Place the cursor on the nearest point on the largest
visible cross section.
//the radius of the largest visible cross section double m = cursorPoint.length(); //cursor's distance from the y-axis
//what we will return as the cursor's 3D location
inBoundsPoint = cursorPoint.times(r/m);
|
| Code Excerpt 1
//Determine whether the selected point is in back or in front
of the largest visible cross
backSide = surfacePoint.y > d;
|
Thereafter, while the user is rotating the solid we keep the cursor on
that same side of the sphere of influence. In other words, if
the cursor was on the front side, we pick the intersection on the
front side and if the cursor was on the back side we pick the
intersection on the back side. We make the following exception:
Each time the user drags the cursor back into bounds after leaving
bounds, we give him control over the other side of the sphere.
By alternating front and back sides this way, we allow the user to
rotate the object full circle (or more) by dragging the cursor back
and forth in and out of bounds. (Code Excerpt 2)
| Code Excerpt 2
//Alternate front and back sides to allow the user to rotate
the solid full circle. Place
//switch to the other side of the sphere of influence
|
| Code Excerpt 3
//a DrawingCanvas member. Possible values are 'x', 'y',
and 'z' for constrained rotation
//Constrain rotation to the x or z-axis. Place this within
DrawingCanvas.mouseDrag to |
Y-axis rotation is enabled whenever the user clicks on a point not on
the virtual object. We assign the cursor a y-coordinate of 0 and
multiply its x- and z-coordinates to keep them on a pre-determined
circle around the origin.
| Code Excerpt 4
//Place within toSurfaceCoord when we discover that the user
has clicked outside of
//a DrawingCanvas member. An arbitrary radius value we use
when theSolid is
//Keeping the cursor's direction from the origin the same,
bring it to the circumference
//remember the new radius of the sphere of influence
//place the coordinate on this sphere |
We continue to do this as the user drags the cursor. (Code Excerpt
5). What the user can't do by hand, we do with a little bit of
code.
| Code Excerpt 5
//Constrain rotation to the y-axis. Place this within
DrawingCanvas.mouseDrag before
//the cursor's 3D coordinates
//if the cursor is on the origin we can't use it |